
So the opposite angles in quadrilateral ACBD are also equal. The angles opposite to equal sides of triangles ∆ABC and ∆ABD are equal. The opposite sides of quadrilateral ∆CBD are equal. The angles between the sides AC, AB and BD, AB are equal. Is ABCD in the figure, a parallelo¬gram? Why? ∠ABC = ∠BDE (The angles opposite to the equal sides of equal triangles are equal) But they are corresponding angles. So the thirif side of triangle are also equal.)
When we consider the triangles ∆CAB, ∆EBD (Corresponding angles)īC = DE (The two sides of ∆ CAB and the angle made by them are equal to the two sides of ∆ EBD and the angle made by them. In the figure below, AC and BE are parallel lines. ∠N = ∠X (If two sides of a triangle are equal, the angles opposite to these sides are also equal) (ii) MN = XY (If two sides of triangle and the angle made by then are equal to two sides of another triangle and the angle made by them, then the third sides of the triangle are also equal) ∴ ∠A = ∠Q (The opposite angles of equal sides of two triangles are also equal) (i) BC = PR (If two sides of a triangle and the angle made by them are equal to two sides of another triangle and the angle made by them, then the third sides of the triangle are also equal.) In each pair of triangles below find the pairs of matching angles and write them down. ∴ ∠BAC = ∠DAC = 30° (Angles opposite to equal sides are equal in a triangle ) ∴ ∠ACD = ∠ACB = 50° (Angles opposite to equal sides of a triangle are equal) The sides of the triangles ABC and ADC are equal. In the quadrilateral ABCD shown below, AB = AD, BC = CDĬompute all the angles of the quadrilateral? You can go online and type the temperature you want to convert into Google using this method: “ 350 degrees F to C” or vice versa. So the angles of ∆ABC are equal to the sides of ∆ABC. The side of ∆ABC are equal to the sides of ∆ABD. The side AB is common to both the triangles in the figure. ∠A = 60, ∠B = 70° then ∠C = 180 – (60° + 70°)Īre the angles of ∆ABC and ∆ABDequal in the figure above? Why? (The angle opposite to equal sides are equal)Ĭompute the remaining angles of both the triangles. Solution: C = 80° (Use the property that the sum of three angles of a triangle is 180°) In the triangles below AB = QR, BC = RP, CA = PQĬompute ∠C of ∆ABC and all angle of ∆PQR. ∠N = ∠X (The angles opposite to the side of length 8cm) ∠M = ∠Z (The angles opposite to the side of length 4 cm) (ii) ∠L = ∠Y (The angles opposite to the sides of length 10cm) ∠C = ∠Q (The angles opposite to the sides of length 6 cm) ∠B = ∠P (The angles opposite to the sides of length 4 cm) (i) ∠A = ∠R (The angles opposite to 5cm sides) In each pair of triangles below, find all pair of matching angles and write them down. Kerala State Syllabus 8th Standard Maths Solutions Chapter 1 Equal Triangles Equal Triangles Text Book Questions and Answers
#Lesson 23 base angles of isosceles triangles download
The vertex angle Y of triangle XYZ equals 8.57 degrees.You can Download Equal Triangles Questions and Answers, Activity, Notes, Kerala Syllabus 8th Standard Maths Solutions Chapter 1 help you to revise complete Syllabus and score more marks in your examinations. Since we know that X = Z because it is an isosceles triangle, then we can solve for the measures of all the angles. First we read "The degree measure of a base angle", so let's start with X= We need to make an equation out of this problem, so let's figure out what it's trying to tell us.

Notice that it's hard to draw a picture without knowing which angles are largest. Find the degree measure of the vertex angle Y. The degree measure of a base angle of isosceles triangle XYZ exceeds three times the degrees measure of the vertex Y by 60. The measure of vertex angle S in triangle RST is 52 degrees. Find the degree measure of the vertex angle S.īase angle + base angle + vertex angle S = 180 degreesĦ4 degrees + 64 degrees + x = 180 degrees Base angles R and T both measure 64 degrees. In isosceles triangle RST, angle S is the vertex angle.

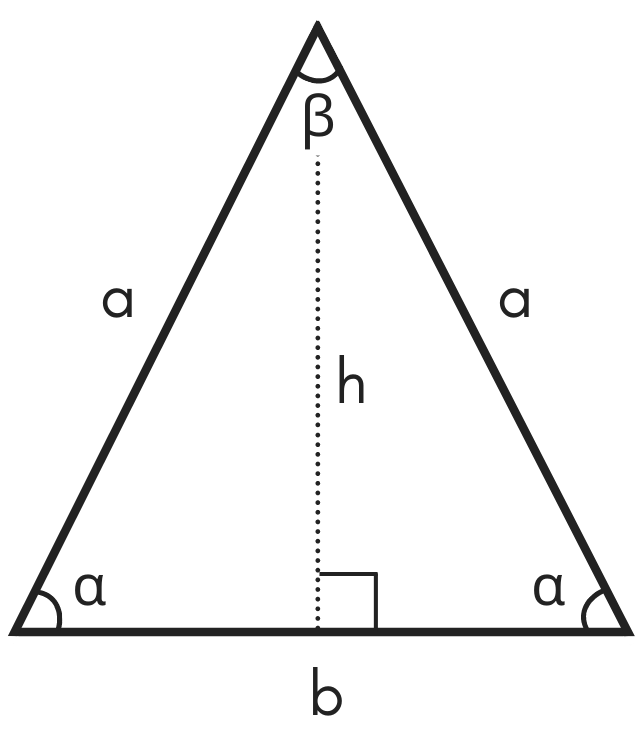
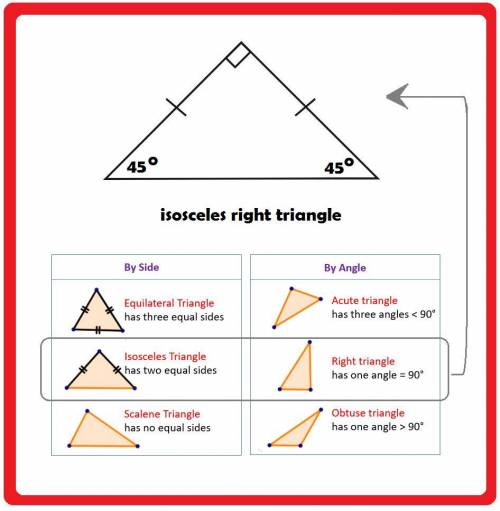
(1) Let x = the measure of each base angle.īase angle + base angle + 120 degrees = 180 degreesĮach base angle of triangle ABC measures 30 degrees. Find the degree measure of each base angle. The vertex angle B of isosceles triangle ABC is 120 degrees. The angle located opposite the base is called the vertex. In an isosceles triangle, we have two sides called the legs and a third side called the base. The easiest way to define an isosceles triangle is that it has two equal sides. Similarly, if two angles of a triangle have equal measure, then the sides opposite those angles are the same length. In an isosceles triangle, the base angles have the same degree measure and are, as a result, equal (congruent). There is a special triangle called an isosceles triangle. There are many types of triangles in the world of geometry.


 0 kommentar(er)
0 kommentar(er)
